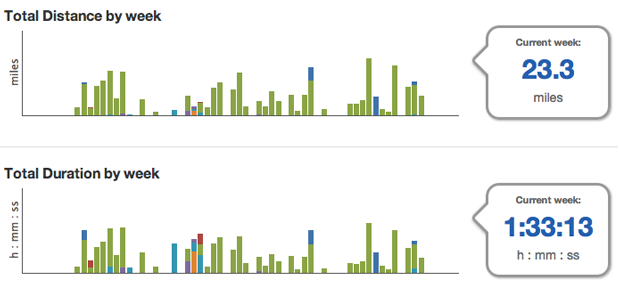
Undeniably, radial charts based on a polar coordinate system are more visually appealing than regular line, area and bar charts, or even tree maps, all of which are based on a cartesian coordinate system. Unfortunately, they are rarely better at communicating information. Radial charts are things like radar charts, Coxcomb charts, radial bar charts, or radial tree maps. 
These charts are all very visually interesting. The have relationships that our brain can easily detect, but that are hard for us to interpret. This duality is why they are more beautiful, but at the same time worse, for showing data. On the other hand, cartesian charts make the data much easier to digest. 
So, why are the cartesian versions better? People’s brains and visual systems are good at seeing straight lines. We are good at comparing two heights if we can see them both at the same time. Even labeling is easier since our text systems are horizontally/vertically based. Each chart has its own issues that can be slightly different from the other charts. Let’s take a look at each one to see why cartesian usually wins.
Radar Charts
Radar charts are basically a line or area chart plotted on polar coordinates. The angle is what in a regular line chart would be the x-axis, and the radius corresponds to the y-axis. In a line chart, the important information is in the height of the points the lines connect, however in a radar chart the important information is now shown by radius. Comparing radii at different angles to each other is cognitively difficult for us, and we judge these distances less accurately than judging heights from a common baseline. One place where these charts are generally seen as acceptable is in small multiples. When used in small multiples, radar charts are usually called star glyphs. Because the task is to compare one to another, the overall shape becomes more important than comparing one dimension to another. This makes radar charts better than line charts for small multiples.
Coxcomb Charts
Coxcomb charts and variations of them are equivalent to column charts. Like in radar charts, angle corresponds to the x-axis and radius, to the y-axis. Coxcomb charts have the same issues with judging height that exist in radar charts, but they also have the addition of disproportionate areas. As a wedge gets a larger radius, the area taken up by the wedge increases disproportionately to the radius increase. Since area also factors into how people judge the size of a chart component, wedges with larger radii are seen as much larger than they are in reality.
Radial Bar Charts
Radial bar charts are the counterpart to a normal bar chart. They also use the same axis translations as Coxcomb and radar charts. The problem with them is that the bars have to be at different radii, so bars on the outside will always take up disproportionately more area than bars on the inside. This means that the only way to judge bar size is angle, unlike the cartesian counterpart where both width and area can be used.
Radial Tree Maps
Radial tree maps are basically the same as an ordinary tree map. But in this case, the translation involves some other differences. The layout in a normal tree map shows the hierarchy in a stacked manner, while in a radial tree map, the hierarchy is shown through splitting the angle of the parent slice on the next concentric ring. This has the same size judgement issues as the bar charts, but because of the overarching structure, the problem is more severe. In a normal treemap, any segment can be compared to any other segment or group of segments. This is because of a part to whole relationship that is maintained through the stacking of the hierarchy. In the radial chart, the part to whole relationship is destroyed. This can make it simpler to see the hierarchy, but harder to compare sizes. In this case, task matters, and on rare occasions a radial tree map may be better than a standard cartesian one. There are a few cases where radial charts are better; small multiples, hierarchy visualization, extremely constrained layouts. Choosing the correct chart for the task is always the important part of creating visualizations, and the same holds true when considering radial charts. If your task isn’t supported better by a radial chart, the data would be better served by going with the cartesian version. Drew Skau is a Visualization Architect at Visual.ly, and a cartesian-minded PhD Computer Science Visualization student at UNCC, with an undergraduate degree in Architecture.
